6502 8 bit PRNG. By Lee Davison.

This is a short peice of code that generates a maximal length, 8 bit, pseudo random number sequence. This is the 6502 version of Z80 random. A 32 bit 68k version can be found here.

This routine is no great shakes in the speed stakes, it's just a demo of a usefull technique.

; returns pseudo random 8 bit number in A. Affects A, X and Y. ; (r_seed) is the byte from which the number is generated and MUST be ; initialised to a non zero value or this function will always return ; zero. Also r_seed must be in RAM, you can see why...... rand_8 LDA r_seed ; get seed AND #$B8 ; mask non feedback bits ; for maximal length run with 8 bits we need ; taps at b7, b5, b4 and b3 LDX #$05 ; bit count (shift top 5 bits) LDY #$00 ; clear feedback count F_loop ASL A ; shift bit into carry BCC bit_clr ; branch if bit = 0 INY ; increment feedback count (b0 is XOR all the ; shifted bits from A) bit_clr DEX ; decrement count BNE F_loop ; loop if not all done no_clr TYA ; copy feedback count LSR A ; bit 0 into Cb LDA r_seed ; get seed back ROL A ; rotate carry into byte STA r_seed ; save number as next seed RTS ; done r_seed .byte 1 ; prng seed byte (must not be zero)

A maximal length pseudo random number generator is basically just a shif register with feedback from the later stages to generate the next input bit. The form for a generator of length n with feedback from t is shown below.

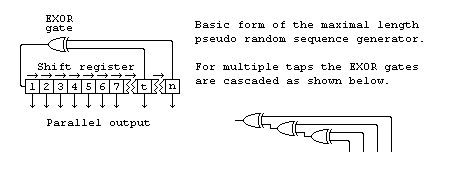
You don't have to limit the length to only 8 bits, any number of bits from two upwards will work if you chose the right feedback tap(s). Here is a table of some values.

Bits [n]	Tap(s) [t]	Length	Bits [n]	Tap(s) [t]	Length
2	1	3	3	2	7
4	3	15	5	3	31
6	5	63	7	6	127
8	6,5,4	255	9	5	511
10	7	1023	11	9	2047
12	11,10,4	4095	13	12,11,8	8191
14	13,12,2	16383	15	14	32767
16	15,13,4	65535	17	14	131071
18	11	262143	19	18,17,14	524287
20	17	1048575	21	19	2097151
22	21	4194303	23	18	8388607
24	23,22,17	16777215	25	22	33554431
28	25	268435455	29	27	536870911
31	28	2147483647

In the last case, with 31 bits, if you took a new value once a second the sequence wouldn't repeat for over sixty eight years. Even clocked at 1MHz it would still take over thirty five minutes to cycle through every state.

The above pseudo random number generator is known as a Fibonacci generator and, while it works, it turns out there is a much better generator to implement with a microprocessor.

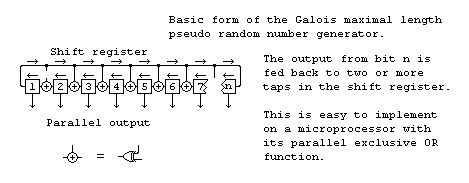
The Galois generator needs only to test the state of one bit and that can be tested after the shift has been performed. The state of this bit determines whether the feedback term is exclusive ORed with the result. This single bit test and multiple bit feedback is easily done as can be seen from the code below.

; returns pseudo random 8 bit number in A. Affects A. (r_seed) is the ; byte from which the number is generated and MUST be initialised to a ; non zero value or this function will always return zero. Also r_seed ; must be in RAM, you can see why...... rand_8 LDA r_seed ; get seed ASL ; shift byte BCC no_eor ; branch if no carry EOR #$CF ; else EOR with $CF no_eor STA r_seed ; save number as next seed RTS ; done r_seed .byte 1 ; prng seed byte, must not be zero

You don't have to limit the length to only 8 bits, any number of bits from three upwards will work if you chose the right feedback value. Here is a table of some values that have been chosen to give a feedback value that fits in a byte, this makes implementation on an 8 bit micro as short as possible. For these values bit n is the least significant bit in the value and the tested bit is the bit shifted out from bit 1.

Bits [n]	Feedback	Length	Bits [n]	Feedback	Length
3	$03	7	4	$03	15
5	$17	31	6	$27	63
7	$4B	127	8	$CF	255
9	$B7	511	10	$E7	1023
11	$EB	2047	12	$EB	4095
13	$BB	8191	14	$BB	16383
15	$DD	32767	16	$D7	65535
17	$AF	131071	18	$E7	262143
19	$AF	524287	20	$F3	1048575
21	$B7	2097151	22	$BB	4194303
23	$F3	8388607	24	$DB	16777215
25	$93	33554431	26	$B1	67108863
27	$B1	134217727	28	$E1	268435455
29	$C3	536870911	30	$AF	1073741823
31	$8B	2147483647	32	$AF	4294967295

This is now the form of sequence generator used to generate values for the RND() function in EhBASIC.

Last page update: 30th July, 2012.

e-mail me