Random numbers are a complex and highly debated subject. The routines presented here use a method known as the linear congruential method. While no method of generating random numbers is perfect, the linear congruential method is widely considered to be a reasonable method. Only the basics of this method will be covered. For further information, the book "The Art Of Computer Programming, Volume 2" by Donald Knuth is highly recommended. Half of the book (chapter 3) covers the topic of random numbers. The strengths and weakness of the common random number generators are discussed, and numerous empirical and theoretical tests for randomness are described. In addition, it suggests several guidelines for random number generators. The book is quite mathematically intense, but it covers random numbers thoroughly.
A pseudo-random number generator does not return an unpredictable number, like rolling a die would. The idea is to take a long sequence of numbers and return them, one by one, in an order that seems random. The key is to start at a random point in this sequence. This starting point is called the seed. The idea is to make sequence long enough so that only a fraction of the sequence will be used when generating random numbers. Then, by starting a random place is the sequence, the fraction of the sequence used will be unlikely to overlap from one run to the next.
Note that by starting with the same seed, the same sequence of numbers can be generated repeatedly. This can be a useful feature.
On the 6502, 8-bit or 16-bit random numbers will be the most common, so the generator will return a 32-bit number. Each of the 2^32 possible values will be returned by the generator, in a seemingly random order, of course.
The term "linear congruential" sounds scary, but there are only two steps involved: multplication and addition. To get the new seed (i.e. the next number in the sequence), the old seed is multiplied by a constant, a, called the multiplier, then a second constant, c, is added to the product. The new seed is the lower 32 bits (remember, this generator returns 32-bit numbers) of the result. (Actually, keeping only the lower 32 bits is really a third step, and in fact, it is an extremely important step.) The computation performed is:
seed = a * seed + c
It turns out that the real key to making a linear congruential generator work is selecting a good value for a, the multiplier. The constant, c, is not as critical as the multiplier, but it must be an odd number. In fact, c can be chosen to be one, and this is what the routines here use, since it will simplify the calculation.
Note that an odd number (the old seed) times an odd number (the multiplier, a) is an odd number, and an odd number (the product) plus an odd number (the constant, c) will be an even number. Likewise, an even number times an odd number, plus an odd number will be an odd number. So the seed will alternate between odd and even numbers. This means that the upper bits of the seed must be used for generating 8-bit and 16-bit random numbers.
The first subroutine is called RAND and it performs the seed = a * seed + 1
(remember, c = 1 was chosen) calculation. There are three versions, a fast
version, a short (in terms of number of bytes) version, and a middle version,
which is between the other two versions in terms of space and speed, yet is
reasonably short and reasonably fast.
The multiplier 1664525 (in hex, $19660D) is used in all three versions. This multiplier was chosen from line 16 of the table on p. 106 of "The Art Of Computer Programming, Volume 2". (That table lists various multipliers and their result in the spectral test, a critical theoretical test for measuring randomness.)
The seed is stored in SEED3 (high byte) through SEED0 (low byte). Putting
SEED3 through SEED0 on the zero page will be faster and shorter (i.e. fewer
bytes), but it is not necessary.
The fast version works by using four pages of pre-computed tables. There are four 256-byte tables, which are named T3, T2, T1, T0.
T3,X = byte X of T3 = bits 31-24 of 1664525 * X, (X = 0 to 255)
T2,X = byte X of T2 = bits 23-16 of 1664525 * X, (X = 0 to 255)
T1,X = byte X of T1 = bits 15-8 of 1664525 * X, (X = 0 to 255)
T0,X = byte X of T0 = bits 7-0 of 1664525 * X, (X = 0 to 255)
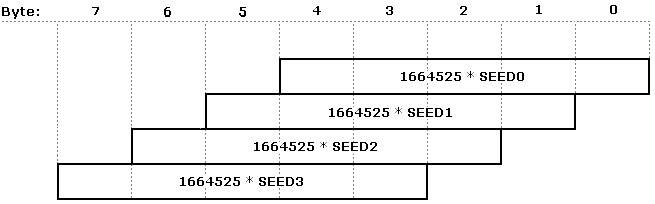
The product of 1664525 * SEED is:

Since only the lowest 4 bytes are kept, the multiplication is: (for brevity, SEED3 to SEED0 are called S3 to S0)

; Linear congruential pseudo-random number generator
;
; Calculate SEED = 1664525 * SEED + 1
;
; Enter with:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; Returns:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; TMP is overwritten
;
; For maximum speed, locate each table on a page boundary
;
; Assuming that (a) SEED0 to SEED3 and TMP are located on page zero, and (b)
; all four tables start on a page boundary:
;
; Space: 58 bytes for the routine
; 1024 bytes for the tables
; Speed: JSR RAND takes 94 cycles
;
RAND CLC ; compute lower 32 bits of:
LDX SEED0 ; 1664525 * ($100 * SEED1 + SEED0) + 1
LDY SEED1
LDA T0,X
ADC #1
STA SEED0
LDA T1,X
ADC T0,Y
STA SEED1
LDA T2,X
ADC T1,Y
STA TMP
LDA T3,X
ADC T2,Y
TAY ; keep byte 3 in Y for now (for speed)
CLC ; add lower 32 bits of:
LDX SEED2 ; 1664525 * ($10000 * SEED2)
LDA TMP
ADC T0,X
STA SEED2
TYA
ADC T1,X
CLC
LDX SEED3 ; add lower 32 bits of:
ADC T0,X ; 1664525 * ($1000000 * SEED3)
STA SEED3
RTS
;
; Generate T0, T1, T2 and T3 tables
;
; A different multiplier can be used by simply replacing the four bytes
; that are commented below
;
; To speed this routine up (which will make the routine one byte longer):
; 1. Delete the first INX instruction
; 2. Replace LDA Tn-1,X with LDA Tn,X (n = 0 to 3)
; 3. Replace STA Tn,X with STA Tn+1,X (n = 0 to 3)
; 4. Insert CPX #$FF between the INX and BNE GT1
;
GENTBLS LDX #0 ; 1664525 * 0 = 0
STX T0
STX T1
STX T2
STX T3
INX
CLC
GT1 LDA T0-1,X ; add 1664525 to previous entry to get next entry
ADC #$0D ; byte 0 of multiplier
STA T0,X
LDA T1-1,X
ADC #$66 ; byte 1 of multiplier
STA T1,X
LDA T2-1,X
ADC #$19 ; byte 2 of multiplier
STA T2,X
LDA T3-1,X
ADC #$00 ; byte 3 of multiplier
STA T3,X
INX ; note: carry will be clear here
BNE GT1
RTS
In the RAND routine, the ADC #1 instruction can be eliminated by calculating
1664525 * X + 1 and storing the result in tables T3I through T0I. SEED0 will
then use TnI (n = 0 to 3) and SEED1 through SEED3 will use Tn. Since table
T3 was only used by SEED0, it (T3) will no longer be necessary. Table T2
will be identical to T2I, so table T2 can also be eliminated. This means
only 6 pages of tables (T0, T1, T0I, T1I, T2I, and T3I) are needed and that
JSR RAND will take 92 cycles.
The short version is just an ordinary 32-bit * 32-bit multiplication routine.
The DB pseudo-op is called .BYTE on some assemblers. Consult the assembler
documentation for the pseudo-op name it expects.
; Linear congruential pseudo-random number generator
;
; Calculate SEED = 1664525 * SEED + 1
;
; Enter with:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; Returns:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; TMP, TMP+1, TMP+2 and TMP+3 are overwritten
;
; Note that TMP to TMP+3 and RAND6 are high byte first, low byte last
;
; Assuming that (a) SEED0 to SEED3 and TMP+0 to TMP+3 are all located on page
; zero, and (b) none of the branches cross a page boundary:
;
; Space: 53 bytes
; Speed: JSR RAND takes 2744 cycles, on average (1624 to 3864 cycles)
; specifically, JSR RAND takes 1624 + 70 * N cycles, where
; N = number of bits of SEED that are 1
;
RAND LDA #1 ; store 1 in TMP
LDX #3
RAND1 STA TMP,X
LSR
DEX
BPL RAND1
LDY #$20 ; calculate SEED = SEED * RAND4 + TMP
BNE RAND5 ; branch always
RAND2 BCC RAND4 ; branch if a zero was shifted out
CLC ; add multiplier to product
LDX #3
RAND3 LDA TMP,X
ADC RAND4,X
STA TMP,X
DEX
BPL RAND3
RAND4 ROR TMP ; shift result right
ROR TMP+1
ROR TMP+2
ROR TMP+3
RAND5 ROR SEED3 ; shift out old seed, and shift in new seed
ROR SEED2
ROR SEED1
ROR SEED0
DEY
BPL RAND2
RTS
RAND6 DB $00,$19,$66,$0D ; multiplier (high byte first!)
Since the carry is known to be set after the BCC RAND4, the CLC can be
eliminated by adding $0019660C instead of $0019660D, saving one byte.
The routine will take one fewer byte if RAND6 (the multiplier) is located on
the zero page. However, since the zero page is usually RAM, RAND6 would have
to be initialized somehow, which would likely nullify the one byte savings.
The middle version is similar to the typical 6502 non-looping multiply-by-10 routines, which are tailored to multiply by a specific number. Unfortunately, this routine must be rewritten if a different multiplier is to be used. The idea to add seed, $100 * seed, $10000 * seed, and/or $1000000 * seed when necessary (as determined by the multiplier), then shift seed (left), and repeat. Specifically,
Bit 0 of $0D (multiplier byte 0) is 1
Bit 0 of $66 (multiplier byte 1) is 0
Bit 0 of $19 (multiplier byte 2) is 1
Bit 0 of $00 (multiplier byte 3) is 0
so, seed is added to $10000 * seed, and seed is shifted left (multiplied by 2)
Bit 1 of $0D is 0
Bit 1 of $66 is 1
Bit 1 of $19 is 0
Bit 1 of $00 is 0
so, $100 * seed is added to the previous result, and seed is shifted left
Bit 2 of $0D is 1
Bit 2 of $66 is 1
Bit 2 of $19 is 0
Bit 2 of $00 is 0
so $100 * seed + seed is added to the previous result, and so on.
; Linear congruential pseudo-random number generator
;
; Calculate SEED = 1664525 * SEED + 1
;
; Enter with:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; Returns:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; TMP, TMP+1, TMP+2 and TMP+3 are overwritten
;
; Assuming that (a) SEED0 to SEED3 and TMP+0 to TMP+3 are all located on page
; zero, and (b) none of the branches cross a page boundary:
;
; Space: 106 bytes
; Speed: JSR RAND takes 517 cycles
;
RAND CLC ; copy SEED into TMP
LDA SEED0 ; and compute SEED = SEED * $10000 + SEED + 1
STA TMP
ADC #1
STA SEED0
LDA SEED1
STA TMP+1
ADC #0
STA SEED1
LDA SEED2
STA TMP+2
ADC TMP
STA SEED2
LDA SEED3
STA TMP+3
ADC TMP+1
STA SEED3
;
; Bit 7 of $00, $19, $66, and $0D is 0, so only 6 shifts are necessary
;
LDY #5
RAND1 ASL TMP ; shift TMP (old seed) left
ROL TMP+1
ROL TMP+2
ROL TMP+3
;
; Get X from the RAND4 table. When:
;
; X = $00, SEED = SEED + $10000 * TMP
; X = $01, SEED = SEED + $100 * TMP
; X = $FE, SEED = SEED + $10000 * TMP + TMP
; X = $FF, SEED = SEED + $100 * TMP + TMP
;
LDX RAND4,Y
BPL RAND2 ; branch if X = $00 or X = $01
CLC ; SEED = SEED + TMP
LDA SEED0
ADC TMP
STA SEED0
LDA SEED1
ADC TMP+1
STA SEED1
LDA SEED2
ADC TMP+2
STA SEED2
LDA SEED3
ADC TMP+3
STA SEED3
INX ; $FE -> $00, $FF -> $01
INX
RAND2 CLC
BEQ RAND3 ; if X = $00, SEED = SEED + TMP * $10000
LDA SEED1 ; SEED = SEED + TMP * $100
ADC TMP
STA SEED1
RAND3 LDA SEED2
ADC TMP,X
STA SEED2
LDA SEED3
ADC TMP+1,X
STA SEED3
DEY
BPL RAND1
RTS
RAND4 DB $01,$01,$00,$FE,$FF,$01
6 cycles (and 1 byte) can be saved by locating the RAND4 table on the zero
page. Since the zero page is usually RAM, RAND4 would have to be
initialized.
Here is an example of the middle routine rewritten for the multiplier 69069 ($10DCD). This multiplier was taken from line 15 of the table on p. 106 of "The Art Of Computer Programming, Volume 2". (According to that table, this multiplier does not do as well on the spectral test as the multiplier 1664525.)
; Linear congruential pseudo-random number generator
;
; Calculate SEED = SEED * 69069 + 1
;
; Enter with:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; Returns:
;
; SEED0 = byte 0 of seed
; SEED1 = byte 1 of seed
; SEED2 = byte 2 of seed
; SEED3 = byte 3 of seed
;
; TMP, TMP+1, TMP+2 and TMP+3 are overwritten
;
; Assuming that SEED0 to SEED3 and TMP+0 to TMP+3 are all located on page
; zero:
;
; Space: 173 bytes
; Speed: JSR RAND takes 326 cycles
;
RAND LDA SEED0 ; TMP = SEED * 2
ASL
STA TMP
LDA SEED1
ROL
STA TMP+1
LDA SEED2
ROL
STA TMP+2
LDA SEED3
ROL
STA TMP+3
CLC ; TMP = TMP + SEED (= SEED * 3)
LDA SEED0
ADC TMP
STA TMP
LDA SEED1
ADC TMP+1
STA TMP+1
LDA SEED2
ADC TMP+2
STA TMP+2
LDA SEED3
ADC TMP+3
STA TMP+3
CLC ; SEED = SEED + $10000 * SEED
LDA SEED2
ADC SEED0
TAX ; keep byte 2 in X for now (for speed)
LDA SEED3
ADC SEED1
TAY ; keep byte 3 in Y for now
CLC ; SEED = SEED + $100 * SEED
LDA SEED1
ADC SEED0
PHA ; push byte 1 onto stack
TXA
ADC SEED1
TAX
TYA
ADC SEED2
TAY
LDA TMP ; TMP = TMP * 4 (= old seed * $0C)
ASL
ROL TMP+1
ROL TMP+2
ROL TMP+3
ASL
ROL TMP+1
ROL TMP+2
ROL TMP+3
STA TMP
CLC ; SEED = SEED + TMP
ADC SEED0
STA SEED0
PLA ; pull byte 1 from stack
ADC TMP+1
STA SEED1
TXA
ADC TMP+2
TAX
TYA
ADC TMP+3
TAY
CLC
LDA TMP ; SEED = SEED + TMP * $100
ADC SEED1
STA SEED1
TXA
ADC TMP+1
TAX
TYA
ADC TMP+2
TAY
LDA TMP ; TMP = TMP * $10 (= old seed * $C0)
ASL ; put byte 0 of TMP in the accumulator
ROL TMP+1
ROL TMP+2
ROL TMP+3
ASL
ROL TMP+1
ROL TMP+2
ROL TMP+3
ASL
ROL TMP+1
ROL TMP+2
ROL TMP+3
ASL
ROL TMP+1
ROL TMP+2
ROL TMP+3
SEC ; SEED = SEED + TMP + 1
ADC SEED0
STA SEED0
LDA TMP+1
ADC SEED1
STA SEED1
TXA
ADC TMP+2
STA SEED2
TYA
ADC TMP+3
STA SEED3
RTS
Having selected a RAND routine, the next step is to turn the new seed into a
(pseudo-)random number. For a random number between 0 and 255 ($FF)
inclusive, simply use SEED3. For a random number between 0 and 65535
($FFFF), use SEED2 for the low byte and SEED3 for the high byte. For a
random number between 0 and 1, use bit 7 of SEED3. For a random number
between 0 and 3, use bits 7 through 6 of SEED3. For a random number between
0 and 7, use bits 7 through 5 of SEED3, and so on. Any random number between
0 and one less than a power of 2 is easily obtained, but what about a random
number between 0 and 5, say? The solution is to multiply SEED by 6 (5 plus
one) and keep the upper 8 bits of the 40-bit product. In this case, 6 is
known as the modulus.
The result is the RANDOM subroutine, which returns a random number, RND,
where 0 <= RND < MOD, and MOD is the modulus. There are two versions of
RANDOM, one for 8-bit RND and MOD, and one for 16-bit RND and MOD. The 8-bit
version, called RANDOM8, is up first, and it uses the number in the
accumulator as the modulus, and returns the random number in the accumulator.
; Linear congruential pseudo-random number generator
;
; Get the next SEED and obtain an 8-bit random number from it
;
; Requires the RAND subroutine
;
; Enter with:
;
; accumulator = modulus
;
; Exit with:
;
; accumulator = random number, 0 <= accumulator < modulus
;
; MOD, TMP, TMP+1, and TMP+2 are overwritten
;
; Note that TMP to TMP+2 are only used after RAND is called.
;
RANDOM8 STA MOD ; store modulus in MOD
JSR RAND ; get next seed
LDA #0 ; multiply SEED by MOD
STA TMP+2
STA TMP+1
STA TMP
SEC
ROR MOD ; shift out modulus, shifting in a 1 (will loop 8 times)
R8A BCC R8B ; branch if a zero was shifted out
CLC ; add SEED, keep upper 8 bits of product in accumulator
TAX
LDA TMP
ADC SEED0
STA TMP
LDA TMP+1
ADC SEED1
STA TMP+1
LDA TMP+2
ADC SEED2
STA TMP+2
TXA
ADC SEED3
R8B ROR ; shift product right
ROR TMP+2
ROR TMP+1
ROR TMP
LSR MOD ; loop until all 8 bits of MOD have been shifted out
BNE R8A
RTS
Here is the 16-bit version of RANDOM, called RANDOM16.
; Linear congruential pseudo-random number generator
;
; Get the next SEED and obtain an 16-bit random number from it
;
; Requires the RAND subroutine
;
; Enter with:
;
; MOD = modulus
;
; Exit with:
;
; RND = random number, 0 <= RND < MOD
;
; TMP is overwritten, but only after RND is called.
;
RANDOM16 JSR RAND ; get next seed
LDA #0 ; multiply SEED by MOD
STA RND+1
STA RND
STA TMP
LDY #16
R16A LSR MOD+1 ; shift out modulus
ROR MOD
BCC R16B ; branch if a zero was shifted out
CLC ; add SEED, keep upper 16 bits of product in RND
ADC SEED0
TAX
LDA TMP
ADC SEED1
STA TMP
LDA RND
ADC SEED2
STA RND
LDA RND+1
ADC SEED3
STA RND+1
TXA
R16B ROR RND+1 ; shift product right
ROR RND
ROR TMP
ROR
DEY
BNE R16A
RTS
There are 2^32 possible values for SEED. When using a modulus that is a
power of 2, each possible value (of RND) returned by RANDOM is equally
likely. However, when modulus of 6 is used, for example, some of the
possible values are a teensy (a very, very teensy) bit more likely than
others, since 2^32 is not a multiple of 6. But 2^32 - 4 is a multiple of 6,
so one solution is to reject four possible values of seed by simply calling
RAND again to get the next seed when one of those four possibilities is
encountered. Since only four values out of 2^32 get rejected, it is highly
unlikely that two consecutive seed values will be rejected, so at most, RAND
will be called twice. The right sequence can ensure that this is so. The
question is, which four values should be rejected?
To answer this question, a simpler example is in order, specifically a 4-bit seed, and a modulus of 7. Since 16-2 is multiple of 7, two values must be rejected. Since there are only 16 possible seed values, all 16 possibilites will be listed, along with the corresponding seed * modulus product.
seed seed * 7 ---- -------- 0000 000 0000 0001 000 0111 0010 000 1110 0011 001 0101 0100 001 1100 0101 010 0011 0110 010 1010 0111 011 0001 1000 011 1000 1001 011 1111 1010 100 0110 1011 100 1101 1100 101 0100 1101 101 1011 1110 110 0010 1111 110 1001
The random numbers (the upper 3 bits of seed * modulus) 0 and 3 occur three times, and the rest occur twice. Notice the lower 4 bits of seed * modulus. When the lower 4 bits are less than 2 (the number of seed values to reject), the upper 3 bits are 000 or 011. Also, when the lower 4 bits are greater than or equal to 16-2, the upper three bits are 000 or 011. This means than there are two ways to determine whether to get the next seed (a) if the lower bits of seed * modulus are less than the number of seed values to reject, or (b) if the lower bits are greater than or equal to 16 minus the number of seed values to reject.
The latter method will be used because it can be implemented little faster. For the 32-bit case, this means checking when the lower 32 bits of the seed * modulus product is less than 2^32 minus the number of seed values to reject. This will be checked by adding the number of seed values to reject to the lower 32 bits of the product and looking for a carry from the 32-bit addition.
The only remaining question is, how many seed values should be rejected? This can be calculated by dividing 2^32 by the modulus. The remainder from this division is the number of seed values to reject.
The subroutine that does all of this is called URANDOM, because it returns a
random number with a uniform distribution. Like RANDOM, it returns a random
number, RND, where 0 <= RND < MOD. There are also two versions, one for
8-bit RND and MOD, and one for 16-bit RND and MOD. The 8-bit version, called
URANDOM8, is once again up first, and it uses the number in the accumulator
as the modulus, and returns the random number in the accumulator.
; Linear congruential pseudo-random number generator
;
; Get the next SEED and obtain an 8-bit uniform random number from it
;
; Requires the RAND subroutine
;
; Enter with:
;
; accumulator = modulus
;
; Exit with:
;
; accumulator = random number, 0 <= accumulator < modulus
;
; MOD, REM, TMP, TMP+1, TMP+2, and TMP+3 are overwritten
;
; Note that TMP to TMP+3 are only used after RAND is called.
;
URANDOM8 STA MOD ; store modulus in MOD
LDX #32 ; calculate remainder of 2^32 / MOD
LDA #1
BNE UR8B
UR8A ASL ; shift dividend left
BCS UR8C ; branch if a one was shifted out
UR8B CMP MOD
BCC UR8D ; branch if partial dividend < MOD
UR8C SBC MOD ; subtract MOD from partial dividend
UR8D DEX
BPL UR8A
STA REM ; store remainder in REM
UR8E JSR RAND
LDA #0 ; multiply SEED by MOD
STA TMP+3
STA TMP+2
STA TMP+1
STA TMP
LDY MOD ; save MOD in Y
SEC
ROR MOD ; shift out modulus, shifting in a 1 (will loop 8 times)
UR8F BCC UR8G ; branch if a zero was shifted out
CLC ; add SEED to TMP
TAX
LDA TMP
ADC SEED0
STA TMP
LDA TMP+1
ADC SEED1
STA TMP+1
LDA TMP+2
ADC SEED2
STA TMP+2
LDA TMP+3
ADC SEED3
STA TMP+3
TXA
UR8G ROR TMP+3 ; shift product right
ROR TMP+2
ROR TMP+1
ROR TMP
ROR
LSR MOD ; loop until all 8 bits of MOD have been shifted out
BNE UR8F
CLC ; add remainder to product
ADC REM
BCC UR8H ; branch if no 8-bit carry
INC TMP ; carry a one to byte 1 of product
BNE UR8H ; branch if no 16-bit carry
INC TMP+1 ; carry a one to byte 2 of product
BNE UR8H ; branch if no 24-bit carry
INC TMP+2 ; carry a one to byte 3 of product
STY MOD ; restore MOD (does not affect Z flag!)
BEQ UR8E ; branch if 32-bit carry
UR8H LDA TMP+3 ; return upper 8 bits of product in accumulator
RTS
Here is the 16-bit version of URANDOM, called URANDOM16.
; Linear congruential pseudo-random number generator
;
; Get the next SEED and obtain an 16-bit random number from it
;
; Requires the RAND subroutine
;
; Enter with:
;
; MOD = modulus
;
; Exit with:
;
; RND = random number, 0 <= RND < MOD
;
; REMH, REML, TEMP, TMP, TMP+1, TMP+2, and TMP+3 are overwritten
;
; Note that TMP to TMP+3 are only used after RAND is called.
;
URANDOM16
LDX #32 ; calculate 2^32 / MOD
LDA #0
STA REMH
SEC ; prepare to shift in a 1
UR16A ROL ; shift dividend left
ROL REMH
BCS UR16B ; branch if a one was shifted out
TAY ; compare partial dividend to MOD
CMP MOD
LDA REMH
SBC MOD+1
TYA
BCC UR16C ; branch if partial dividend < MOD
UR16B SBC MOD ; subtract MOD from paritial dividend (computes remainder)
TAY
LDA REMH
SBC MOD+1
STA REMH
TYA
CLC
UR16C DEX
BPL UR16A
STA REML ; store low byte of remainder in REM
LDA MOD+1 ; save high byte of MOD in TEMP
STA TEMP
UR16D JSR RAND
LDA MOD ; save low byte of MOD in TMP+3
STA TMP+3
LDA #0 ; multiply SEED by MOD
STA RND+1
STA RND
STA TMP+2
STA TMP+1
LDY #16
UR16E LSR MOD+1 ; shift out modulus
ROR MOD
BCC UR16F ; branch if a zero was shifted out
CLC ; add SEED, keep upper 16 bits of product in RND
TAX
LDA TMP+1
ADC SEED0
STA TMP+1
LDA TMP+2
ADC SEED1
STA TMP+2
LDA RND
ADC SEED2
STA RND
LDA RND+1
ADC SEED3
STA RND+1
TXA
UR16F ROR RND+1 ; shift product right
ROR RND
ROR TMP+2
ROR TMP+1
ROR TMP
ROR
DEY
BNE UR16E
CLC ; add remainder to product
ADC REML
LDA TMP
ADC REMH
BCC UR16G ; branch if no 16-bit carry
INC TMP+1 ; carry a one to byte 2 of product
BNE UR16G ; branch if no 24-bit carry
LDA TMP+3 ; restore MOD
STA MOD
LDA TEMP
STA MOD+1
INC TMP+2 ; carry a one to byte 3 of product
BEQ UR16D ; branch if 32-bit carry
UR16G RTS
URANDOM16 could be sped up slightly by replacing the SEC instruction with a LDA #1 instruction followed by a branch (BNE) to the first TAY instruction. Then, the ROL at UR16A can be changed to an ASL, and the CLC just before UR16C can be deleted.
Finally, here is a routine that allows the RAND routine to be accessed via the USR function in EhBASIC. Rbyte4 through RByte1 (the seed for the RND function) could be used for SEED3 through SEED0 as follows:
SEED0 = Rbyte4
SEED3 = SEED0+1
SEED2 = SEED0+2
SEED1 = SEED0+3
Note that Rbyte4 through Rbyte1 are not in order in memory! The downside to
using Rbyte is if RND and USR are both used. The RND seed (Rbyte) cannot be
all zeros, or RND will always return 0, but an all zero seed is perfectly
fine for a linear congruential generator. (EhBASIC cleverly avoids an all
zeros seed by setting the seed only on a non-zero argument to RND.) SEED3
through SEED0 could use unused zero page locations (such as $DE to $E1) or
other unused RAM elsewhere instead.
FAC1_1 is used for TMP, since it and the next 3 locations (FAC1_2, FAC1_3,
and FAC1_s) are overwritten after the JSR RAND anyway. FAC1_e could also
be used since the next 3 locations are FAC1_1, FAC1_2, and FAC1_3.
Since the usage of USR is identical to that of RND, RND can simply be
replaced by USR. Remember, before using USR, the statement DOKE 11,address
(where address is the address of the routine below) must be used to set
the USR vector.
; USR-based linear congruential pseudo-random number generator
;
; Usage is identical to RND
;
; Requires the RAND subroutine
;
TMP = FAC1_1
LDA FAC1_e ; get FAC1 exponent
BEQ USRNG_1 ; do next random # if zero
LDX #<SEED0 ; set PRNG pointer low byte
LDY #>SEED0 ; set PRNG pointer high byte
JSR LAB_2778 ; pack FAC1 into (XY)
USRNG_1
JSR RAND ; get the next random number
LDX #$02 ; three bytes to copy
USRNG_2
LDA SEED3,X ; get PRNG byte
STA FAC1_1,X ; save FAC1 byte
DEX
BPL USRNG_2 ; loop if not complete
LDA SEED0 ; set the rounding byte
STA FAC1_r
LDA #$80 ; set the exponent
STA FAC1_e ; save FAC1 exponent
ASL ; clear A
STA FAC1_s ; save FAC1 sign
JMP LAB_24D5 ; normalize FAC1 & return
Last page update: January 30th, 2005.